通过矩阵来研究二次函数(方程),这就是线性代数中二次型的重点。 1 二次函数(方程)的特点 1.1 二次函数 最简单的一元二次函数就是: 给它增加一次项不会改变形状: 增加常数项就更不用说了,更不会改变形状。 ...
AI小编归纳总结**矩阵魔法:二次型的几何诗篇** 二次函数与方程的精髓藏在"二次项"里,如同画布上决定轮廓的浓墨。一元或多元,增减线性项如同调节阴影,而二次矩阵才是图形的基因密码。 用对称矩阵编码二次型,数学家的魔法就此展开: - **圆锥曲线协奏曲**:圆、椭圆、双曲线竟是同一支线性变换舞曲的不同节拍,三维圆锥与平面相遇的刹那,矩阵悄然书写着它们的血缘。 - **扶正的艺术**:歪斜的椭圆?特征值分解如执剑,劈开旋转与拉伸,正交矩阵为尺,对角矩阵为墨,顷刻绘出端正的几何图腾。 - **正定的启示**:矩阵特征值皆为正时,函数图像如碗承露;若含负值,则成马鞍驰骋。半正定似碗中浅水,不定者如风暴中的海面。 线性代数以矩阵为透镜,将二次型的几何之美折射为代数光谱,在数学宇宙中织就璀璨星图。 [本文内容由人工智能深度求索 - DeepSeek辅助生成,仅供参考] 通过矩阵来研究二次函数(方程),这就是线性代数中二次型的重点。 1 二次函数(方程)的特点 1.1 二次函数 最简单的一元二次函数就是: 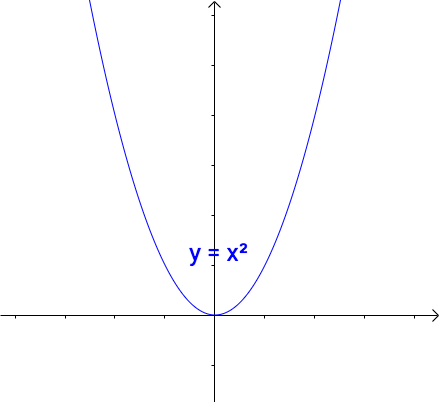 给它增加一次项不会改变形状: 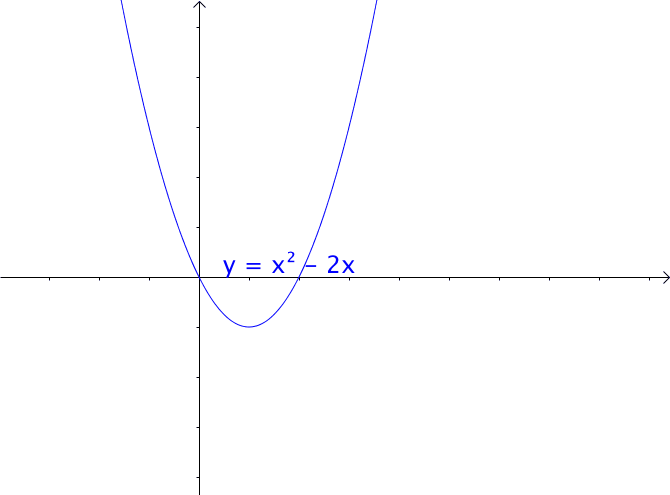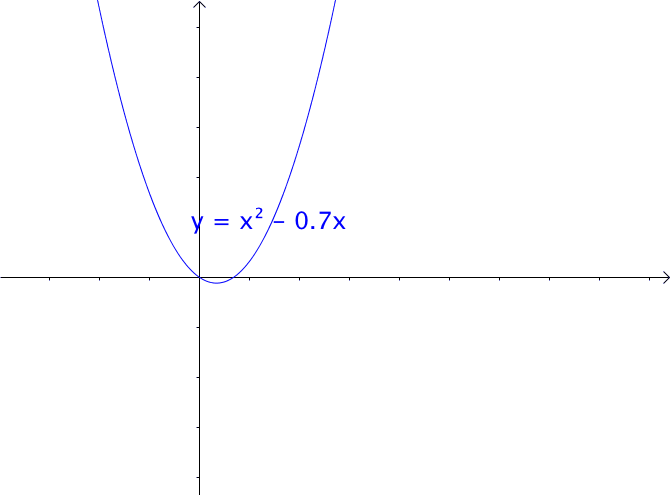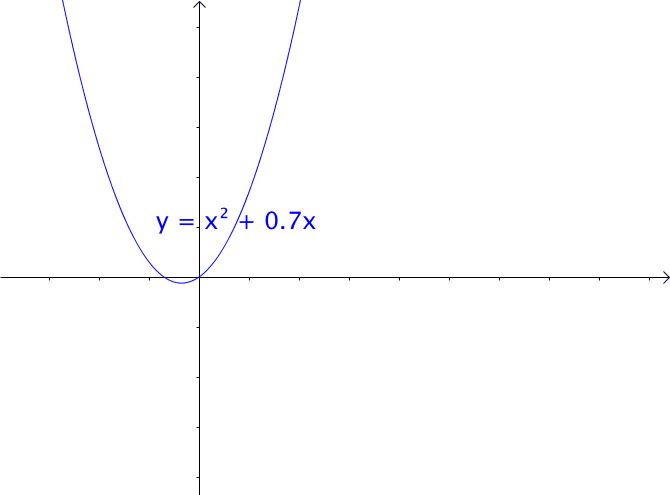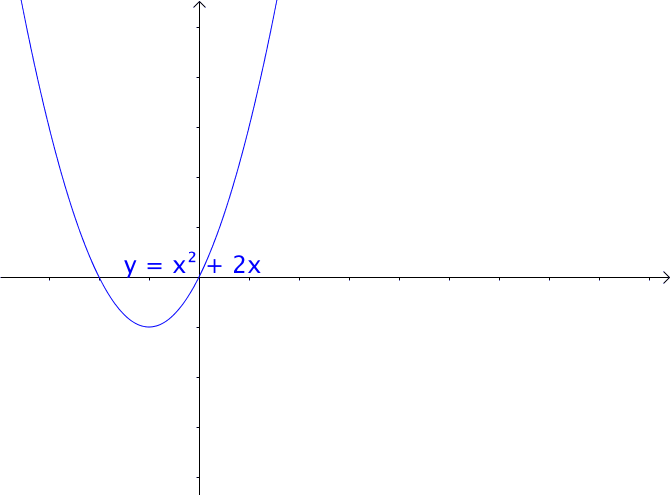 增加常数项就更不用说了,更不会改变形状。 1.2 二次方程 下面是一个二元二次方程: 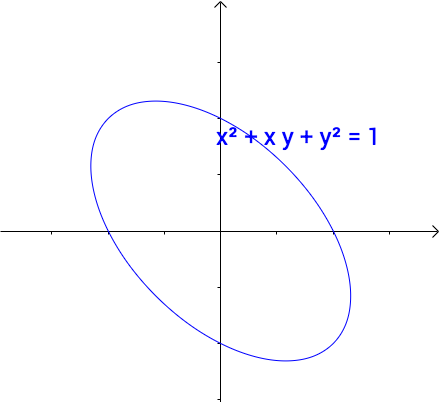 给它增加一次项也不会改变形状,只是看上去有些伸缩: 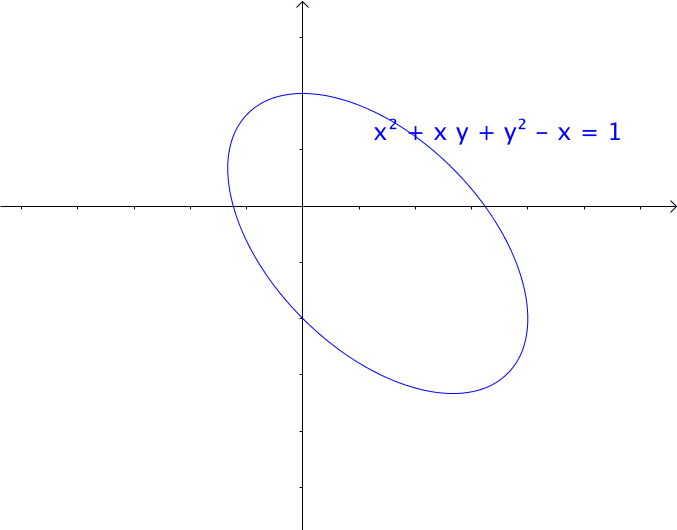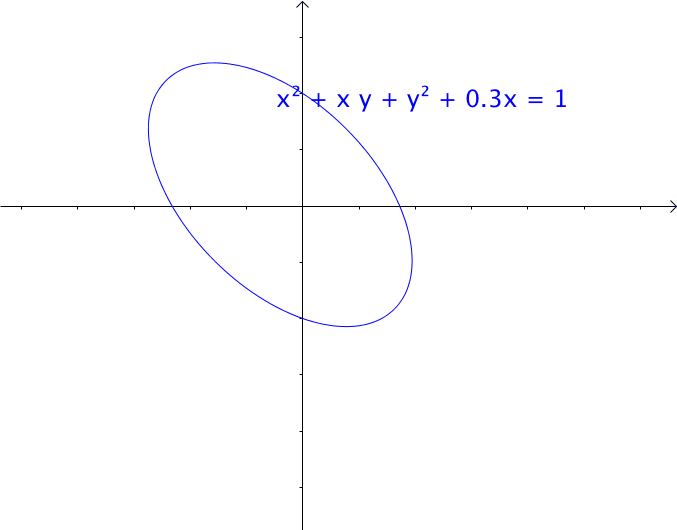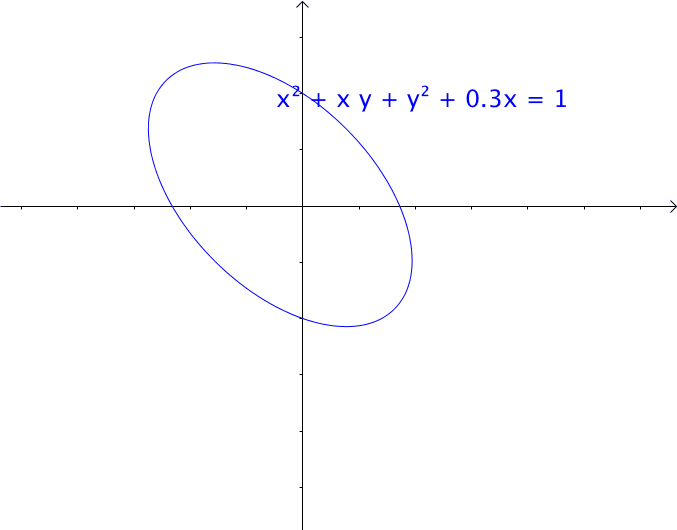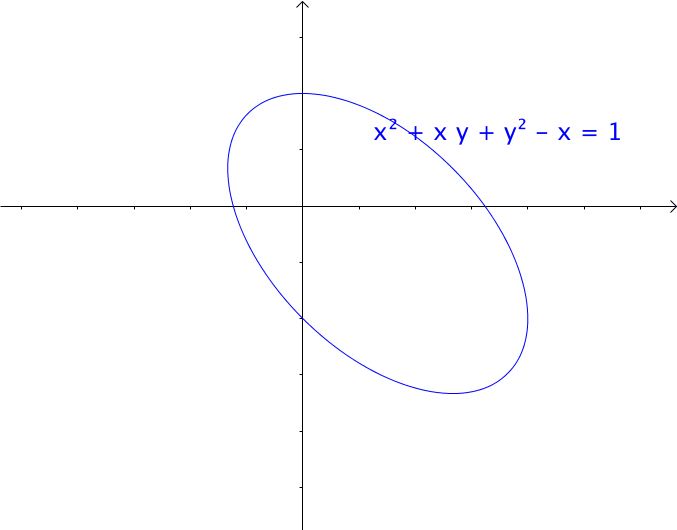 1.3 小结 对于二次函数或者二次方程,二次部分是主要部分,往往研究二次这部分就够了。 2 通过矩阵来研究二次方程 因为二次函数(方程)的二次部分最重要,为了方便研究,我们把含有 个变量的二次齐次函数: 称为二次型。 2.1 二次型矩阵 实际上我们可以通过矩阵来表示二次型: 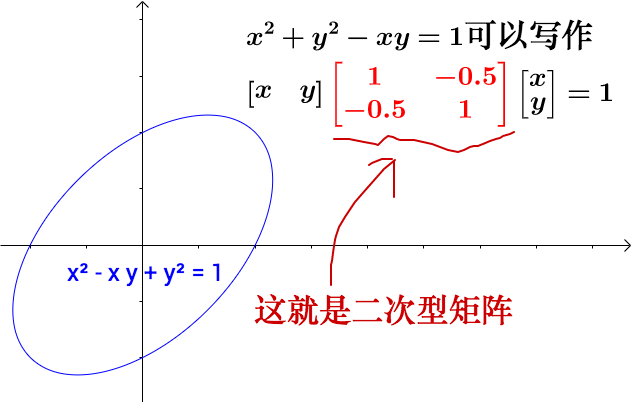 更一般的:  可以写成更线代的形式: 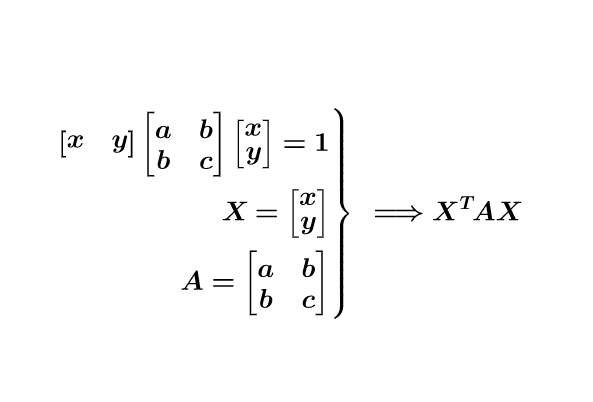 所以有下面一一对应的关系: 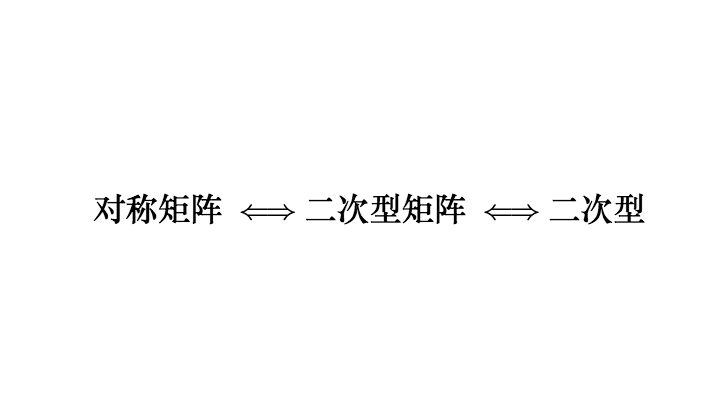 在线代里面,就是通过一个对称矩阵,去研究某个二次型。 2.2 通过矩阵来研究有什么好处 2.2.1 圆锥曲线 我们来看下,这是一个圆: 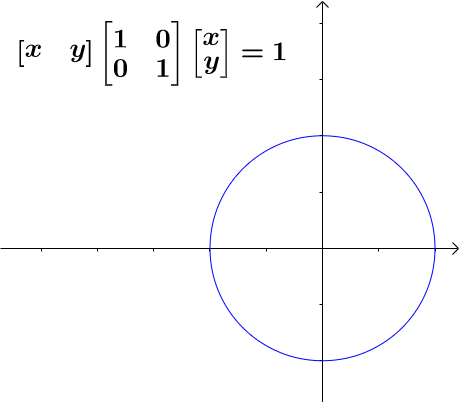 我们来看改变一下二次型矩阵: 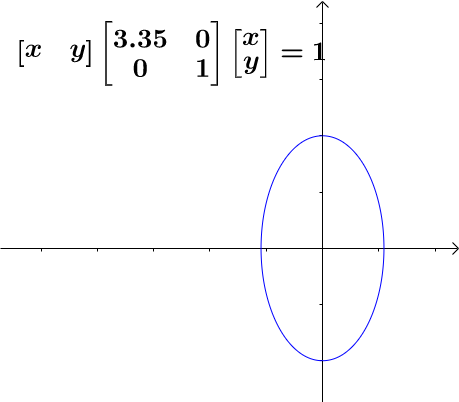 哈,原来椭圆和圆之间是线性关系呐(通过矩阵变换就可以从圆变为椭圆)。 继续: 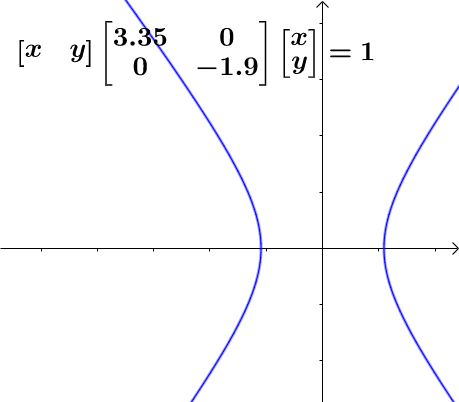 咦,双曲线和圆之间也是线性关系。 其实圆、椭圆、双曲线之间关系很紧密的,统称为圆锥曲线,都是圆锥体和平面的交线: 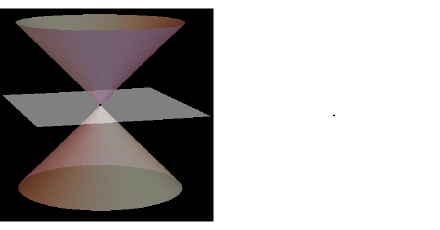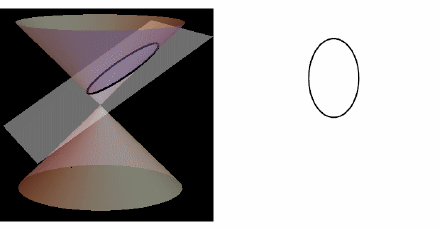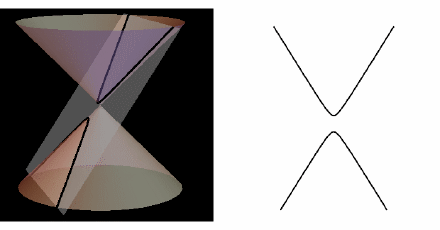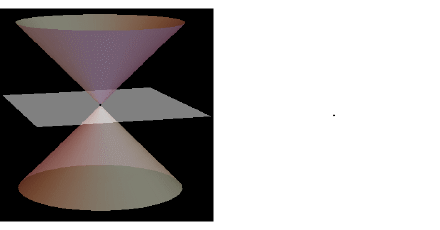 从上面动图可看出,一个平面在圆锥体上运动,可以得到圆、椭圆、双曲线,这也是它们之间具有线性关系的来源(平面的运动实际上是线性的)。 2.2.2 规范化 再改变下矩阵: 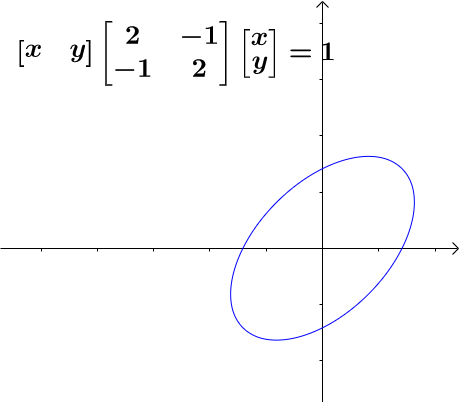 这个椭圆看起来有点歪,不太好处理,我们来把它扶正,这就叫做规范化。 如果我们对矩阵有更深刻的认识,那么要把它扶正很简单。 往下读之前,请先参看我在 如何理解特征值 下的回答。 首先,矩阵代表了运动,包含:
对于方阵,因为没有维度的改变,所以就没有投影这个运动了,只有:
具体到上面的矩阵: 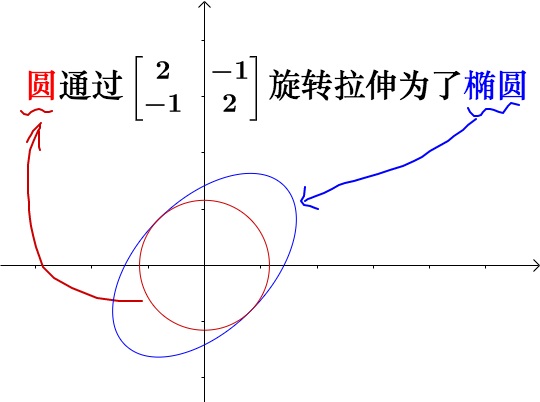 我把这个矩阵进行特征值分解: 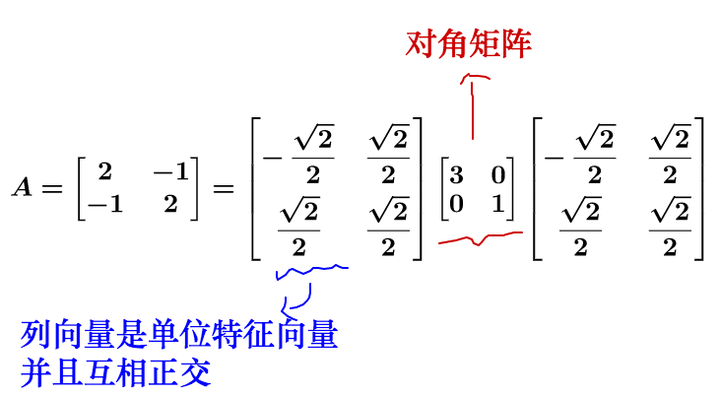 注意我上面提到的正交很重要,为什么重要,可以参看我在 如何理解特征值 。 对于二次型矩阵,都是对称矩阵,所以特征值分解总可以得到正交矩阵与对角矩阵。 特征值分解实际上就是把运动分解了: 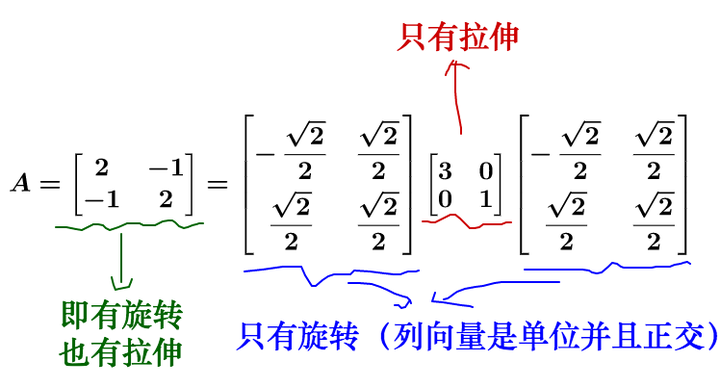 那么我们只需要保留拉伸部分,就相当于把矩阵扶正(图中把各自图形的二次型矩阵标注出来了): 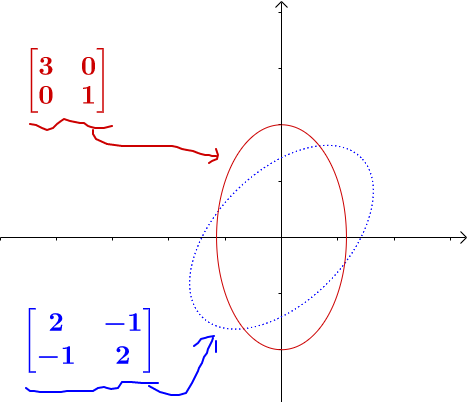 所以,用二次型矩阵进行规范化是非常轻松的事情。 2.2.3 正定 正定是对二次函数有效的一个定义,对方程无效。 对于二次型函数, :
从图像上看,这是正定: 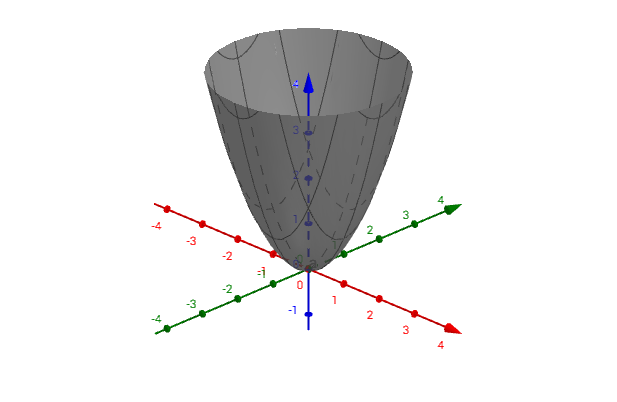 半正定: 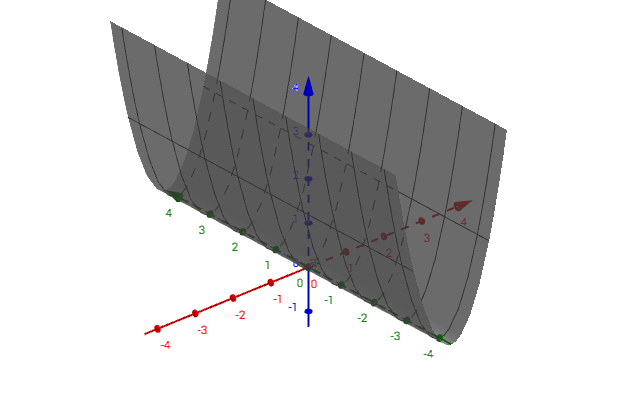 不定: 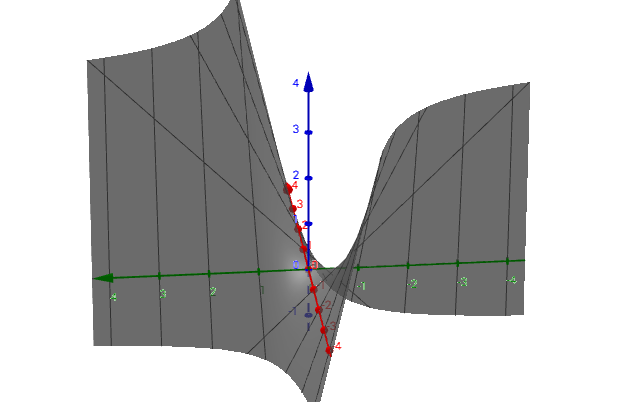 既然二次型用矩阵来表示了,那么我们能否通过矩阵来判断是否正定呢? 下面我分别给出了二次型的图形,以及对应的特征值矩阵的图形,你可以自己动手试试(3D 窗口可以通过鼠标旋转,方便观察),得出自己的结论: 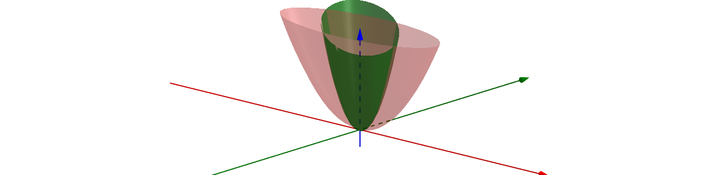 此处有互动内容,点击此处前往操作。 起码,我们可以观察出这个结论,特征值都大于 0,则为正定矩阵。 3 总结 在很多学科里,二次型都是主要研究对象,很多问题都可以转为二次型。线代作为一门数学工具,在二次型的研究中也发挥了很好的作用。 最新版本(可能有后继更新):如何理解二次型? 更多内容推荐【马同学图解数学】系列 |
**矩阵魔法:二次型的几何诗篇** 二次函数与方程的精髓藏在"二次项"里,如同画布上决定轮廓的浓墨。一元或多元,增减线性项如同调节阴影,而二次矩阵才是图形的基因密码。 用对称矩阵编码二次型,数学家的魔法就此展开: - **圆锥曲线协奏曲**:圆、椭圆、双曲线竟是同一支线性变换舞曲的不同节拍,三维圆锥与平面相遇的刹那,矩阵悄然书写着它们的血缘。 - **扶正的艺术**:歪斜的椭圆?特征值分解如执剑,劈开旋转与拉伸,正交矩阵为尺,对角矩阵为墨,顷刻绘出端正的几何图腾。 - **正定的启示**:矩阵特征值皆为正时,函数图像如碗承露;若含负值,则成马鞍驰骋。半正定似碗中浅水,不定者如风暴中的海面。 线性代数以矩阵为透镜,将二次型的几何之美折射为代数光谱,在数学宇宙中织就璀璨星图。 [本文内容由人工智能深度求索 - DeepSeek辅助生成,仅供参考]